गोलगणकस्य आयतनम्
गोलस्य आयतनं गणयितुं त्रिज्या अथवा व्यासदीर्घतां निवेशयन्तु ।
आयतनगणकाः
- ओज to ml(द्रव औंसं मिलीलीटररूपेण परिवर्तयन्तु)
- घनरूपगणकस्य आयतनम्: आयताकारप्रिज्मस्य आयतनस्य गणनां कुर्वन्तु

- गोलगणकस्य आयतनम्: गोलस्य आयतनं गणयन्तु
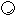
इदं एकं गणकयंत्रं यत् विशेषतया एकस्य सेफेरस्य अथवा एकस्य कन्दुकस्य आयतनस्य गणनां करोति , समर्थनं मेट्रिकं तथा शाही-एककं (इञ्च, पादं, गजं, मिमी, सेमी वा मीटर्), आयतनपरिणामं च भिन्न-एककं परिवर्तयितुं शक्नोति, गणनासूत्रेण गतिशील-दृश्येन च सह sphere, अस्मान् उत्तराणि प्राप्तुं परिणामान् च अधिकसुलभतया अवगन्तुं साहाय्यं करोति।
अस्य गणकस्य उपयोगः कथं करणीयः ?
- आयतनस्य गणनाय व्यासस्य अथवा त्रिज्यायाः उपयोगं कर्तुं चिनोतु ।
- व्यासस्य वा त्रिज्यायाः वा दीर्घतां निवेशयन्तु
- निवेशदशमलवं वा भिन्नं वा स्वीकुरुत, उदा. ३.४, १.७, ५ १/४ वा ३/५
- व्यासस्य अथवा त्रिज्यायाः एककं चिनुत
- भवन्तः यत् आयतनस्य एककं ज्ञातुम् इच्छन्ति तत् चिनुत
- स्वयमेव परिणामानां गणनां करिष्यति, अन्तरक्रियाशीलरूपेण प्रतिक्रियां च करिष्यति ।
- गणनायाः परिणामः गोलः भविष्यति।
गोलस्य आयतनं कथं गणनीयम् ?
गोलः सम्यक् गोल ज्यामितीयः वस्तु अस्ति यः त्रिविमः भवति, यस्य पृष्ठे प्रत्येकं बिन्दुः तस्य केन्द्रात् समदूरे भवति । कन्दुकं वा भूमण्डलं वा इत्यादयः बहवः सामान्यतया प्रयुक्ताः पदार्थाः गोलाः सन्ति । यदि भवान् गोलस्य आयतनं गणयितुम् इच्छति तर्हि केवलं तस्य त्रिज्याम् अन्विष्य सरलसूत्रे प्लग् करणीयम्,
वि = 4⁄3πr3।
गोला आयतन सूत्र
गोलस्य आयतनस्य सूत्रं घनत्रिज्यायाः ४/३ गुणा pi गुणा भवति । सङ्ख्यायाः घनीकरणस्य अर्थः भवति यत् तस्याः स्वयमेव त्रिगुणं गुणनं भवति, अस्मिन् सति त्रिज्या गुणा त्रिज्या गुणा भवति ।
गोलाकार आयतन = 4⁄3 × π × त्रिज्या × त्रिज्या × त्रिज्या
πवृत्तस्य परिधिव्यासस्य अनुपातः इति
गणना उदाहरणम्
४ इञ्च् त्रिज्यायुक्तस्य गोलस्य आयतनं ज्ञातव्यम् ।
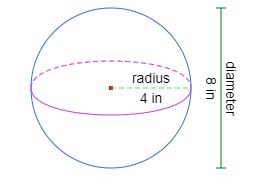
४ ÷ ३ × ३.१४१५९२६५३५८९७९३ × ४ × ४ × ४ = २६८.०८२५७३१०६३२९ ।
गोलीकरणानन्तरं तस्य आयतनं २६८.०८ घनइञ्च् भवति ।
यदि वयं आयतनस्य एककान् भिन्न-भिन्न-एककेषु परिवर्तयितुम् इच्छामः तर्हि प्रथमं त्रिज्या-एककान् आयतनस्य समाने परिवर्तयितुं शक्नुमः,
उदाहरणतया,
९ इञ्च् त्रिज्यायुक्तं गोलम् ।
ft3 मध्ये तस्य आयतनं किम् ?
४ ÷ ३ × ३.१४१५९२६५३५८९७९३ × ०.७५ × ०.७५ × ०.७५ = १.७६७१४५८६७६४४२५८४
गोलीकरणानन्तरं तस्य आयतनं १.७७ घनफीट् भवति ।
यदि अस्माकं केवलं व्यासस्य संख्या अस्ति तर्हि अर्धव्यासः त्रिज्या अस्ति, केवलं व्यासस्य 2 इत्यनेन विभज्य त्रिज्या भविष्यति ।