घनरूपगणकस्य आयतनम्
आयतनगणकाः
- ओज to ml(द्रव औंसं मिलीलीटररूपेण परिवर्तयन्तु)
- घनरूपगणकस्य आयतनम्: आयताकारप्रिज्मस्य आयतनस्य गणनां कुर्वन्तु

- गोलगणकस्य आयतनम्: गोलस्य आयतनं गणयन्तु
इदं एकं गणकयंत्रं यत् विशेषतया घनरूपस्य आयतनस्य गणनां करोति, समर्थनमेट्रिक-इम्पेरियल्-एककानां (इञ्च्, पाद-गज, मि.मी., से.मी. वा मीटर्) गणयति, आयतनपरिणामः च भिन्न-एककेषु परिवर्तयितुं शक्नोति, गणनासूत्रेण गतिशील-दृश्यघनेन च, तत् उत्तराणि प्राप्तुं परिणामान् अधिकसुलभतया अवगन्तुं च अस्मान् साहाय्यं करोति।
अस्य गणकस्य उपयोगः कथं करणीयः ?
- संख्याः दीर्घतायाः, विस्तारस्य, ऊर्ध्वतायाः च रिक्तस्थानेषु निवेशयन्तु
- निवेशदशमलवं वा भिन्नं वा स्वीकुरुत, उदा. २.६, ७.८, ४ १/२ वा ३/५
- भवन्तः यत् मापस्य एककं प्रयुञ्जते तत् चिनुत (in, ft, yd, mm, cm, m) ।
- यत् परिणामस्य एककं भवन्तः इच्छन्ति तत् चिनुत
- स्वयमेव परिणामानां गणनां करिष्यति, अन्तरक्रियाशीलरूपेण प्रतिक्रियां च करिष्यति ।
- गणनायाः परिणामः गोलः भविष्यति।
घनरूपस्य आयतनं कथं गणनीयम्
घनरूपः एकः ठोसः पेटी अस्ति यस्य प्रत्येकं पृष्ठं समानक्षेत्रस्य अथवा भिन्नक्षेत्रस्य आयतः भवति ।
घनरूपस्य दीर्घता, विस्तारः, ऊर्ध्वता च भविष्यति ।
घनरूपस्य आयतनम् = (दीर्घता × विस्तार × ऊर्ध्वता) घन-एककाः ।
आयत आयतन सूत्र
गणना उदाहरणम्
14 सेमी × 12 सेमी × 8 सेमी आयामस्य घनरूपस्य आयतनं ज्ञातव्यम् ।
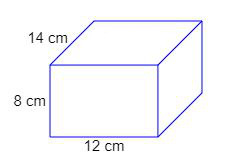
= 1344 घन सेमी.
अतः घनरूप का आयतन = १३४४ घन सेमी.
यदि वयं आयतनस्य एककान् भिन्न-भिन्न-एककेषु परिवर्तयितुम् इच्छामः तर्हि प्रथमं आयामानां एककान् आयतनस्य समाने परिवर्तयितुं शक्नुमः,
उदाहरणतया,
घनस्य परिमाणं १२.५ इञ्च्, १४ इञ्च्, ९.३ इञ्च् च भवति ।
ft3 मध्ये तस्य आयतनं किम् ?
१४ इञ्च् = १४ ÷ १२ पाद = १.१६७ पाद
९.३ इञ्च् = ९.३ ÷ १२ फीट् = ०.७७५ फीट्
१.०४२ × १.१६७ × ०.७७५ इञ्च = ०.९४२४१०८५ फीट्३
गोलीकरणानन्तरं आयतनं ०.९४ इञ्च् फीट्३ भवति
घनरूपं घनत्वं च
एकःघनरूपःपेटीरूपं वस्तु अस्ति । षट् समतलमुखाः सर्वे समकोणाः सन्ति । तस्य च सर्वाणि मुखानि आयतानि सन्ति। अस्य दीर्घतायाः समानः क्रॉस्-सेक्शन् भवति इति कारणतः अपि प्रिज्मः अस्ति । वस्तुतः आयताकारः प्रिज्मः अस्ति ।
यदा त्रयोऽपि दीर्घाः समानाः भवन्ति तदा क उच्यतेघन(अथवा षट्कोणः) प्रत्येकं मुखं च वर्गः भवति। घनः अद्यापि प्रिज्मः घनरूपः अपि अस्ति ।