Ҳаҷми ҳисобкунаки сфера

=
Браузери шумо теги canvas HTML5 -ро дастгирӣ намекунад.

Барои ҳисоб кардани ҳаҷми кура радиус ё дарозии диаметрро ворид кунед.

Ҳисобкунакҳои ҳаҷми

Ин ҳисобкунакест, ки махсусан ҳаҷми сефера ё тӯбро ҳисоб мекунад, воҳидҳои метрӣ ва империалиро (дюйм, фут, ярд, мм, см ё метр) дастгирӣ мекунад ва натиҷаи ҳаҷм метавонад бо формулаи ҳисоб ва визуалии динамикӣ ба воҳиди гуногун табдил ёбад. соҳа, он ба мо кӯмак мекунад, ки ҷавоб гирем ва натиҷаҳоро осонтар фаҳмем.

Ин ҳисобкунакро чӣ тавр истифода бурдан мумкин аст?

  1. Барои ҳисоб кардани ҳаҷм истифода бурдани диаметр ё радиусро интихоб кунед.
  2. Дарозии диаметр ё радиусро ворид кунед
  3. Даҳҳо ё касрҳои воридшударо қабул кунед, масалан. 3,4, 1,7, 5 1/4 ё 3/5
  4. Воҳиди диаметр ё радиусро интихоб кунед
  5. Воҳиди ҳаҷмро, ки мехоҳед бидонед, интихоб кунед
  6. Он ба таври худкор натиҷаҳоро ҳисоб мекунад ва ба таври интерактивӣ вокуниш нишон медиҳад.
  7. Натиҷаи ҳисоб мудаввар карда мешавад.

Ҳаҷми кураро чӣ гуна ҳисоб кардан мумкин аст?

Сфера як объекти геометрии комилан мудавварест, ки се андоза дорад ва ҳар як нуқтаи рӯи он аз марказаш баробар аст. Бисёре аз объектҳои маъмулан истифодашаванда ба монанди тӯбҳо ё глобусҳо сфера мебошанд. Агар шумо хоҳед, ки ҳаҷми кураро ҳисоб кунед, шумо бояд радиуси онро пайдо кунед ва онро ба формулаи оддӣ пайваст кунед,
V = 4⁄3πr³.

Формула ҳаҷми сфера

Формулаи ҳаҷми кура 4/3 маротиба pi ба радиуси куб аст. Мукааб кардани адад маънои онро ба худ се маротиба зарб кардан аст, дар ин ҳолат радиус ба радиус бо радиус аст.

V = 4⁄3πr³
Ҳаҷми кура = 4⁄3 × π × радиус × радиус × радиус
πтаносуби доираи доира ба диаметри он мебошад

Намунаи ҳисобкунӣ

Ҳаҷми кураи радиусаш 4 дюймро ёбед.

Ҳаҷм = 4⁄3π4³
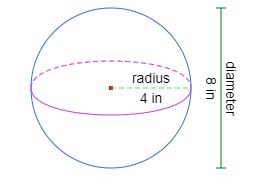
4 ÷ 3 × 3,141592653589793 × 4 × 4 × 4 = 268,082573106329.
Пас аз яклухткунӣ, ҳаҷм 268,08 дюймаи мукааб аст.

Агар мо хоҳем, ки воҳидҳои ҳаҷмро ба воҳидҳои гуногун табдил диҳем, мо метавонем аввал воҳидҳои радиусро ба ҳамон ҳаҷм табдил диҳем,
барои намуна,
кура бо радиусаш 9 дюйм.
Ҳаҷми он дар фут3 чанд аст?

радиус 9 дюйм = 9 ÷ 12 фут = 0,75 фут Ҳаҷм = 4⁄3π0,75³
4 ÷ 3 × 3,141592653589793 × 0,75 × 0,75 × 0,75 = 1,7671458676442584
пас аз яклухт, ҳаҷми 1,77 метри мукааб аст.

Агар мо танҳо рақами диаметр дошта бошем, нисфи диаметри радиус аст, танҳо диаметрро ба 2 тақсим кунем ва мо радиусро хоҳем дошт.