ປະລິມານເຄື່ອງຄິດເລກແບບສະເຟຍ
ປ້ອນລັດສະໝີ ຫຼືຄວາມຍາວເສັ້ນຜ່າສູນກາງເພື່ອຄຳນວນປະລິມານຂອງວົງມົນ.
ເຄື່ອງຄິດໄລ່ປະລິມານ
- Oz ກັບ ml(ປ່ຽນອໍສຂອງນໍ້າເປັນມິນລີລິດ)
- ປະລິມານເຄື່ອງຄິດເລກ cuboid: ຄິດໄລ່ປະລິມານຂອງ prism ສີ່ຫລ່ຽມ

- ປະລິມານເຄື່ອງຄິດເລກແບບສະເຟຍ: ຄິດໄລ່ປະລິມານຂອງສະເຟຍ
ນີ້ແມ່ນເຄື່ອງຄິດໄລ່ໂດຍສະເພາະແມ່ນການຄິດໄລ່ປະລິມານຂອງ sephere ຫຼືບານ, ສະຫນັບສະຫນູນຫນ່ວຍວັດແລະ imperial (ນິ້ວ, ຕີນ, yards, mm, cm ຫຼືແມັດ) ແລະຜົນໄດ້ຮັບປະລິມານທີ່ສາມາດປ່ຽນເປັນຫນ່ວຍງານທີ່ແຕກຕ່າງກັນ, ມີສູດການຄິດໄລ່ແລະພາບເຄື່ອນໄຫວ. ຜ່ານ, ມັນຊ່ວຍໃຫ້ພວກເຮົາໄດ້ຮັບຄໍາຕອບແລະເຂົ້າໃຈຜົນໄດ້ຮັບງ່າຍຂຶ້ນ.
ໃຊ້ເຄື່ອງຄິດເລກນີ້ແນວໃດ?
- ເລືອກໃຊ້ເສັ້ນຜ່າສູນກາງຫຼືລັດສະໝີເພື່ອຄິດໄລ່ປະລິມານ.
- ໃສ່ຄວາມຍາວຂອງເສັ້ນຜ່າສູນກາງຫຼືລັດສະໝີ
- ຍອມຮັບການປ້ອນຂໍ້ມູນເລກທົດສະນິຍົມ ຫຼືເສດສ່ວນ, ຕົວຢ່າງ. 3.4, 1.7, 5 1/4 ຫຼື 3/5
- ເລືອກຫົວໜ່ວຍຂອງເສັ້ນຜ່າສູນກາງ ຫຼື ລັດສະໝີ
- ເລືອກຫົວໜ່ວຍປະລິມານທີ່ເຈົ້າຢາກຮູ້
- ມັນຈະຄິດໄລ່ຜົນໄດ້ຮັບໂດຍອັດຕະໂນມັດແລະປະຕິກິລິຍາໂຕ້ຕອບ.
- ຜົນໄດ້ຮັບຂອງການຄິດໄລ່ຈະເປັນຮູບກົມ.
ວິທີການຄິດໄລ່ປະລິມານຂອງສະເຟຍ?
ຊົງກົມເປັນວັດຖຸເລຂາຄະນິດທີ່ຊົງກົມຢ່າງສົມບູນ, ເປັນສາມມິຕິ, ໂດຍທຸກຈຸດຢູ່ດ້ານຂອງມັນຢູ່ຫ່າງກັນຈາກສູນກາງຂອງມັນ. ວັດຖຸທີ່ໃຊ້ທົ່ວໄປຫຼາຍອັນເຊັ່ນ: ບານ ຫຼື ໜ່ວຍໂລກເປັນຮູບຊົງກົມ. ຖ້າຫາກວ່າທ່ານຕ້ອງການທີ່ຈະຄິດໄລ່ປະລິມານຂອງວົງ, ທ່ານພຽງແຕ່ມີການຊອກຫາ radius ຂອງຕົນແລະສຽບມັນເປັນສູດງ່າຍດາຍ,
V = 4⁄3πr³.
ສູດປະລິມານສະເຟຍ
ສູດສໍາລັບປະລິມານຂອງຮູບຊົງກົມແມ່ນ 4/3 ເທົ່າ pi ເທົ່າກັບ radius cubed. Cubing a number ຫມາຍຄວາມວ່າການຄູນມັນດ້ວຍຕົວມັນເອງສາມຄັ້ງ, ໃນກໍລະນີນີ້, ລັດສະໝີຄູນກັບ radius ເທົ່າກັບ radius.
ບໍລິມາດສະເຟຍ = 4⁄3 × π × ລັດສະໝີ × ລັດສະໝີ × ລັດສະໝີ
πແມ່ນອັດຕາສ່ວນຂອງວົງມົນຂອງວົງມົນກັບເສັ້ນຜ່າສູນກາງຂອງມັນ
ຕົວຢ່າງການຄິດໄລ່
ຊອກຫາປະລິມານຂອງວົງມົນທີ່ມີລັດສະໝີ 4 ນິ້ວ.
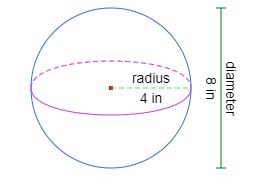
4 ÷ 3 × 3.141592653589793 × 4 × 4 × 4 = 268.082573106329 .
ຫຼັງຈາກຮອບ, ປະລິມານແມ່ນ 268.08 ລູກບາດນິ້ວ.
ຖ້າຫາກວ່າພວກເຮົາຕ້ອງການທີ່ຈະປ່ຽນຫົວຫນ່ວຍຂອງປະລິມານເປັນຫົວຫນ່ວຍທີ່ແຕກຕ່າງກັນ, ພວກເຮົາສາມາດປ່ຽນຫົວຫນ່ວຍຂອງ radius ເປັນປະລິມານດຽວກັນກ່ອນ,
ຍົກຕົວຢ່າງ,
ວົງກົມທີ່ມີລັດສະໝີ 9 ນິ້ວ.
ປະລິມານຂອງມັນຢູ່ໃນ ft³ ແມ່ນຫຍັງ?
4 ÷ 3 × 3.141592653589793 × 0.75 × 0.75 × 0.75 = 1.7671458676442584 .
ຫຼັງຈາກຮອບ, ປະລິມານແມ່ນ 1.77 ລູກບາດຟຸດ.
ຖ້າເຮົາມີພຽງແຕ່ເສັ້ນຜ່າກາງເທົ່ານັ້ນ, ເສັ້ນຜ່າກາງເຄິ່ງໜຶ່ງແມ່ນລັດສະໝີ, ພຽງແຕ່ແບ່ງເສັ້ນຜ່າກາງດ້ວຍ 2, ເຮົາຈະມີລັດສະໝີ.